磁化構造に起因する異常ホール効果とスピンホール効果
ホール効果
金属や半導体に電場をかけたとき,通常は電場の方向にしか電流は発生しません. しかし,電場と垂直な方向に磁場をかけた場合,電子がローレンツ力を感じることによって,電場と磁場の双方に垂直な方向に電流(電圧)が生じることが知られています. この現象をホール効果と呼び,ホール素子をはじめとした磁場検出法の一つとして多様な応用がなされ,私たちの日常生活を支えています.(絶縁体における量子ホール効果はこちらを参照) また,磁場がなくてもホール効果が起こる物質も存在し,そのような現象はしばしば異常ホール効果と呼ばれます. ホール効果と異常ホール効果は,19世紀末にE. W. Hallの実験によって同時期に発見されました [1,2]. この異常ホール効果は強磁性体において発見され,電子スピンの一様分極と,スピン軌道相互作用による(↑スピンと↓スピンの)非対称散乱という量子力学的機構によって説明されます(図1左). ところが,発見当時は量子力学の理解が進んでおらず,発見から約70年後にようやくこのような理論的説明がなされました [3].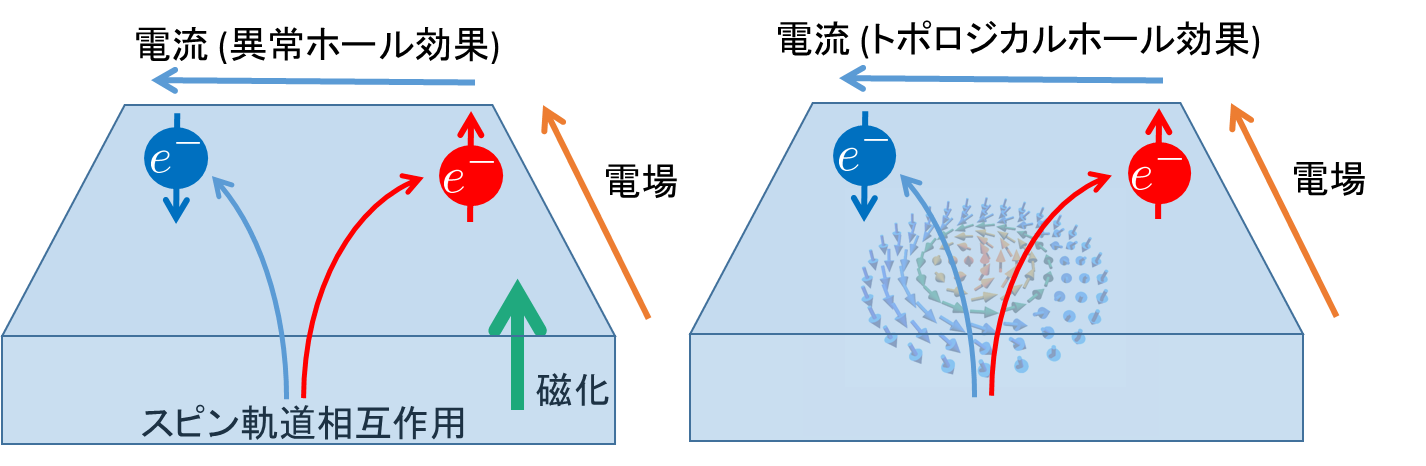
図1:(左)異常ホール効果の概念図. スピン軌道相互作用によって↑スピンと↓スピンが非対称に散乱され,かつ磁化が存在して↑スピンと↓スピンの数が異なると,全体として電荷の流れ(電流)が生じる. (右)(強結合の場合の)トポロジカルホール効果の概念図. ↑スピンと↓スピンが逆向きの有効磁場を感じ,非対称に散乱されることでホール効果が生じる.
スピンカイラリティーに誘起されるホール効果:トポロジカルホール効果
それからさらに約半世紀後,磁性体中のスピンカイラリティーという局在磁化の非共面的な構造(図2)もホール効果を誘起するのではないかという提案がなされました [4]. この現象は現在トポロジカルホール効果と呼ばれ,伝導電子スピンが局在磁化との交換相互作用を介して有効磁場を感じるというメカニズムで理解されています. このような磁化構造はスカーミオン(図3) [5],磁気渦 [6],スピングラス [7]などとして存在しますが,スピントロニクスの観点では特にスカーミオンが情報担体として注目されており,トポロジカルホール効果はその検出法として注目されています [8].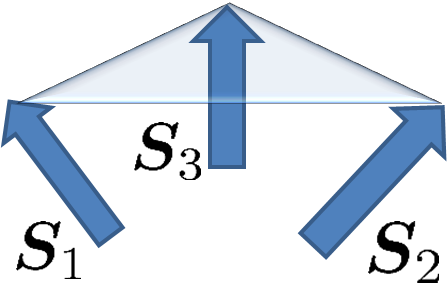
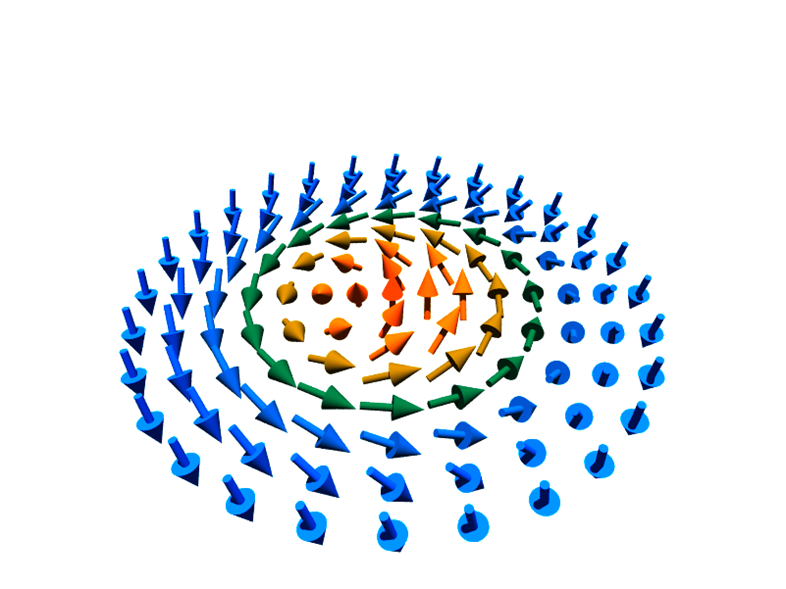
図2(左):スピンカイラリティーをもつ磁化構造. 図3(右):(磁気)スカーミオン.
トポロジカルホール効果:強結合から弱結合まで
このトポロジカルホール効果はこれまで,ベリー位相という数学的表現と関連付けて説明されてきました [9]. このベリー位相による解釈は,伝導電子の伝搬過程で電子状態を変えない(バンド間遷移が起こらない)場合によい描像を与えます. 今の場合,伝導電子スピンと局在磁化の交換相互作用が強く(強結合領域),局在磁化の空間変化が十分遅い(長波長の)場合にベリー位相の描像は成立し,異常ホール効果の時と同様に伝導電子の非対称散乱として説明することができます(図1右). ところが,交換相互作用が弱い場合(弱結合)や,局在磁化の空間変化が速い(短波長の)場合にはベリー位相の描像は破綻します. さらに,ベリー位相で解釈する場合には,有効磁場は局所的な磁化構造で決まりますが,先ほどの弱結合の場合には有効磁場は磁化構造と非局所的な関係 [10]で決まることがあります. これまでは,強結合領域と弱結合領域はそれぞれ独立に調べられていましたが,私たちはゲージ場の方法という枠組みを用いてホール伝導度の解析的表式を導き,強結合から弱結合までを統一的に説明しました. その結果,これまで調べられてこなかった「中間結合領域」が存在し,この領域に有効磁場の「局所-非局所」の境界があることを見出しました [11]. また,この中間結合領域におけるホール伝導度の表式が,Mn酸化物における巨大なトポロジカルホール効果の実験を定性的に説明することもわかりました [12].トポロジカルホール効果:長波長から短波長まで
私たちは,微小振幅の方法や,交換相互作用の摂動といった方法でも解析を行い,先ほどのゲージ場による計算を定性的に支持する結果を得ました. また,交換相互作用の摂動を用いて短波長の領域でも計算を行い,特にスカーミオン格子におけるトポロジカルホール効果の特徴的な振る舞いを明らかにしました.反強磁性体におけるトポロジカルホール効果
反強磁性体では,上向きと下向きの磁化が共線的に並んでいるため,この共線的磁化構造(Neelベクトル)が空間変化しても,互いに逆向きのカイラリティーが常に存在するので,ホール効果は起きません. ところが,この共線的磁化が少し傾いた場合(キャントした反強磁性体,図4),その磁化構造はスピンカイラリティーをもつ可能性があります. 私達は,キャントした反強磁性体において、緩やかに空間変化するスピンテクスチャに対しHall伝導度を計算し, その結果,一様磁化の一次で磁化構造に起因するHall効果の表式を得ました(in preparation).
図4:非共線的な磁化構造.
反強磁性体におけるトポロジカルスピンホール効果
先ほど,共線的磁化構造によってトポロジカルホール効果が起きないことを説明しましたが,(強結合の極限では)逆向きのスピンカイラリティーは↑スピンと↓スピンにそれぞれ逆向きの軌道運動を与えるので,スピンホール効果が期待されます. 私たちは現在,このようなNeelベクトルのカイラリティーによるスピンホール効果の微視的に理解することに取り組んでいます.- E. H. Hall, Am. J. Math. 2, 287 (1879).
- E. H. Hall, Philos. Mag. 12, 157 (1881).
- R. Karplus and J. M. Luttinger. Phys. Rev. 95, 1154 (1954), J. Smit, Physica (Amsterdam) 21, 877 (1955).
- J. Ye , Y. B. Kim, A. J. Millis, B. I. Shraiman, P. Majumdar, and Z. Tešanović, Phys. Rev. Lett. 83, 3737 (1999).
- S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, P. Böni, Science, 323, 915 (2009).
- T. Shinjo, T. Okuno, R, Hassdorf, K. Shigeto, and T. Ono, Science 289, 930 (2000).
- H, Kawamura, J. Phys. Soc. Jpn. 79, 011007 (2010).
- A. Fert, V. Cros, and J. Sampaio, Nature nanotech. 8, 152 (2013).
- M. V. Berry, Proc. R. Soc. London A 392, 45 (1984).
- G. Tatara and H. Kawamura, J. Phys. Soc. Jpn. 71, 2613 (2002), K. Nakazawa and H. Kohno, J. Phys. Soc. Jpn. 83, 073707 (2014).
- K. Nakazawa, M. Bibes and H. Kohno, J. Phys. Soc. Jpn. 87, 033705 (2018).
- L. Vistoli, W.Wang, A. Sander, Q. Zhu, B. Casals, R. Cichelero, A. Barthélémy, S. Fusil, G. Herranz, S. Valencia, R. Abrudan, E. Weschke, K. Nakazawa, H. Kohno, J. Santamaria, W. Wu, V. Garcia, and M.Bibes, Nature Phys. (2018).
