量子ホール効果とトポロジー

波動関数が非自明なトポロジーを示す系はトポロジカル物質と呼ばれています．その最も代表的な例は磁場中の二次元電子系であり，そのトポロジカル量子現象は量子ホール効果です．

系に印加した電場（y方向とする）E_y に対してその直交方向に電流 j_x が誘起される現象がホール効果ですが，面直方向の磁場 (B_z) 中の二次元電子系においては，そのホール伝導率 σ_xy が e²/h を単位として整数に量子化される，すなわち，Nを整数として σ_xy = j_x/E_y = N e²/h となることが1980年に報告されました[1]．興味深いことに，この現象は非常に高い精度（10桁程度）で観測され，現在では抵抗標準としても用いられています．この業績により，発見者のKlaus von Klitzingは1985年にノーベル物理学賞を受賞しています．

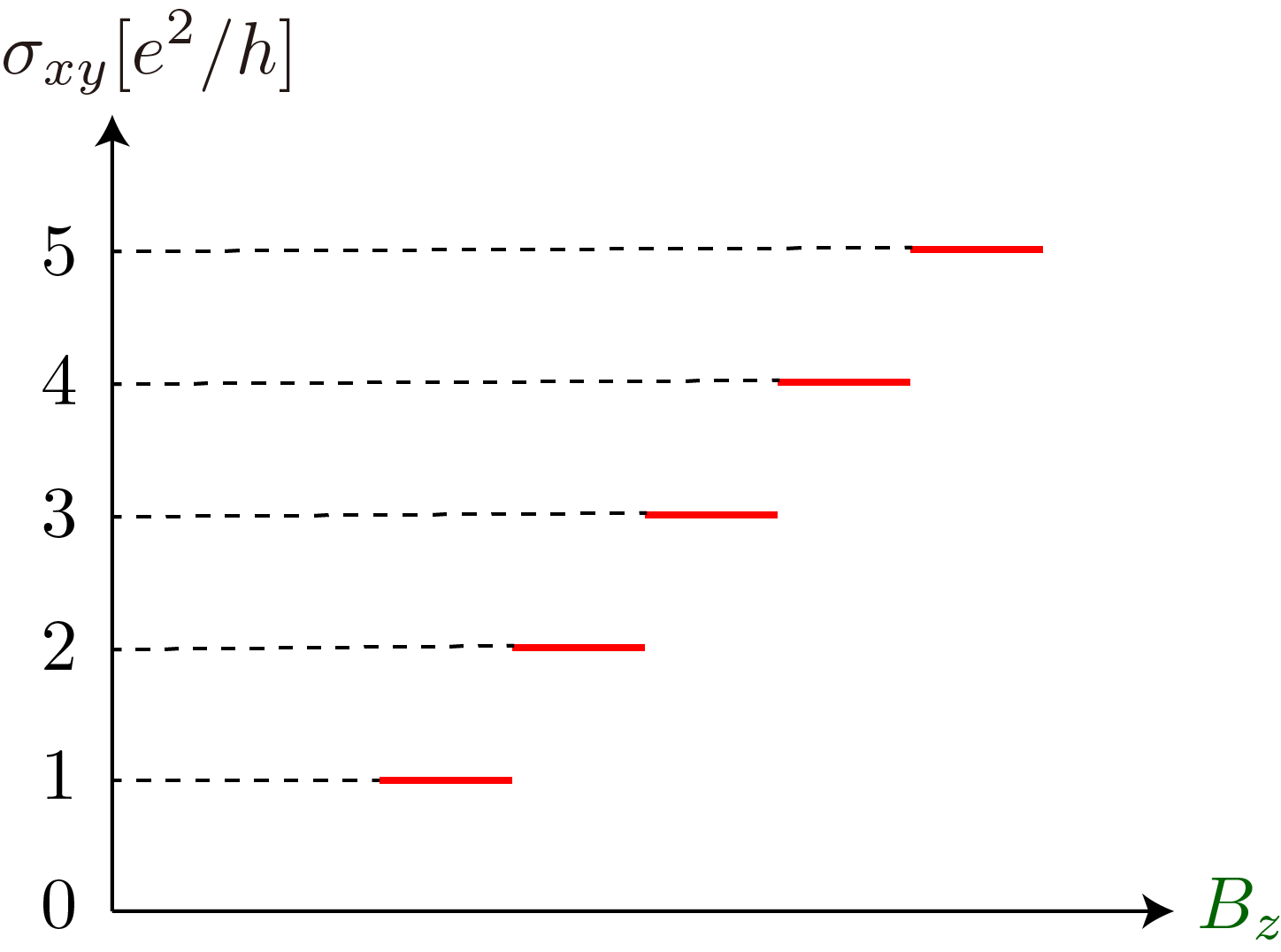
実は量子ホール効果というのはトポロジーに起因するものであることが，その後の研究により明らかにされました．ホール伝導率は線形応答理論により求められますが，これをさらに以下の形に表現できることが Thouless-Kohmoto-Nightingale-den Nijs [2] により示されています．

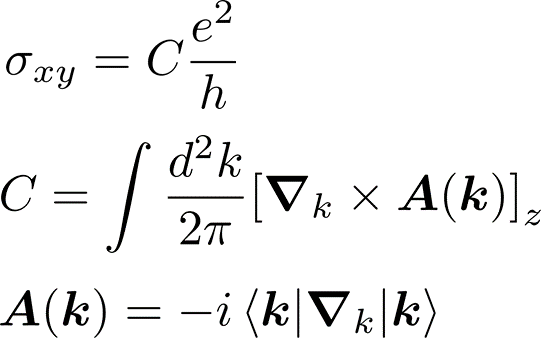
CはTKNN数と呼ばれる整数であり，また，数学におけるトポロジカル不変量の一つであるチャーン数と同じ形になっています[3]．またラフリンによって別な形での量子ホール効果のトポロジカルな議論もなされています[4]．

このように，量子ホール効果はトポロジカル不変量として表現されることは，単なる式の書き換えに留まるものではなく，現象の本質的理解を与えています．トポロジカル不変量は連続変形に対して値を変えない量でした．物理の言葉で言い直せば，これは系に対する多少の摂動に対して，ホール伝導率 σ_xy は全く値を変えないことを意味します．これは取りも直さず，量子ホール効果が実験的に非常に高い精度で観測される理論的な裏付となっているのです．

量子ホール効果がトポロジカルな量子現象であることが分かると，これ以外にもトポロジカルな物質相があるのではないか，という自然な疑問が生じます．実際にこの点について様々な研究が成され，最終的には2015年に大きな転機が訪れました．トポロジカル絶縁体の発見です．

1. K. v. Klitzing, G. Dorda, and M. Pepper, Phys. Rev. Lett. 45, 494 (1980).
2. D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49, 405 (1982).
3. M. Kohmoto, Ann. Phys. 160, 343 (1985).
4. R. B. Laughlin, Phys. Rev. B 23, 5632(R) (1981).