名古屋大学 理学研究科

物性理論研究室 量子輸送理論グループ（S研 Stグループ）

トポロジカル絶縁体と表面状態

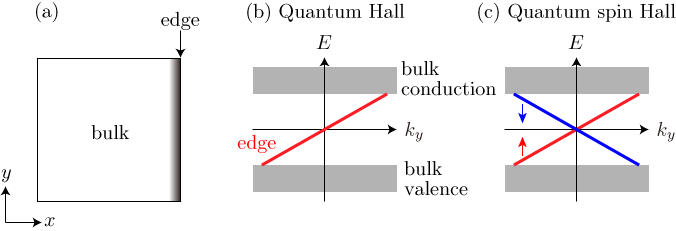
トポロジカル絶縁体の普遍的な特徴として，系の表面に必ずギャップレスの状態が現れます．二次元のトポロジカル絶縁体を考えてみましょう．絶縁体であるので，エネルギーバンドにはギャップが開いています．しかし，下図(a)のように，x=0に端がある系におけるエネルギースペクトルは下図(b),(c)のようにバンドギャップ中にギャップレスのモードをもっているのです．

トポロジカル物質の重要な概念として，バルク・端対応があります[1]． 量子ホール系のトポロジカル不変量はチャーン数でした．実は，

（チャーン数）＝（右進行波のギャップレス端状態の数）－（左進行波のギャップレス端状態の数）

という関係式が成り立ちます．左辺のチャーン数はバルクの波動関数から計算される，すなわち，端とは全く関係なく決まる量ですが，これが端状態の数を与えるという驚くべき結果です．一般に，端がある有限系の計算は難しいですが，これを実行する代わりに，より簡単なバルクの計算で済むのです．上の関係により，この端状態はトポロジカルに保護された極めて安定な状態であり，乱れなどによって破壊されることはありません．

バルク・端対応は全てのトポロジカル物質で同様に成立します．量子ホール系の場合には，前述のように，右向き（あるいは左向き）のみに進行するカイラルな端状態，量子スピンホール系の場合にはスピン↑が右向き，スピン↓が左向き，というように，ヘリカルな端状態が存在しています．すなわち，量子ホール系の端には電流，量子スピンホール系の端にはスピン流が散逸することなく永久に流れていることになります．

さらに三次元のトポロジカル絶縁体においても同様に，バルクのトポロジカル不変量により必ず系の表面にギャップレスの状態が現れます．その波動関数は

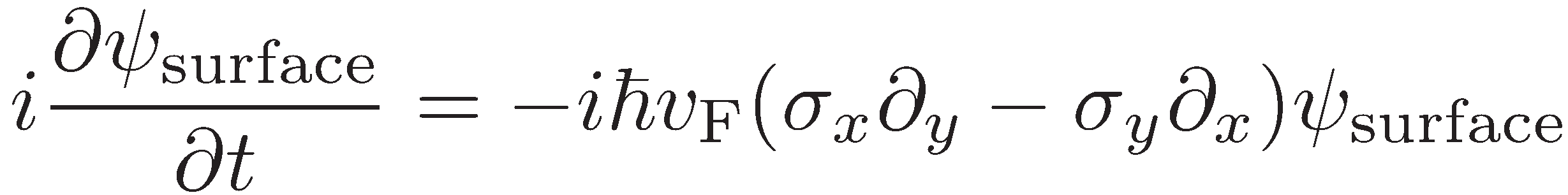
という零質量の二次元のディラック方程式に従うため，通常の金属とは全く異なる性質を示します．例えば，この表面の金属状態は系がどんなに強く乱れていても決してアンダーソン局在を起こしません［２］．これに起因して，系の易動度が非常に高くなることが予想されます．トポロジカル絶縁体は低消費電力デバイスの応用材料という観点からも興味深い系です．

我々もトポロジカル絶縁体の表面状態について，以下のような研究を行っています．

  1. トポロジカル絶縁体における表面状態の解析解

    半無限系における表面に束縛された状態のエネルギーと波動関数の解析解を構成する系統的な方法を提案．また，ジグザグ状の端においてはトポロジカル由来のものとは別に，更に余分に表面状態が現れることを指摘．

    1. K.-I. Imura, A. Yamakage, S. Mao, A. Hotta and Y. Kuramoto, "Zigzag edge modes in Z2 topological insulator: reentrance and completely flat spectrum," Phys. Rev. B 82, 085118 (2010).
    2. S. Mao, Y. Kuramoto, K.-I. Imura, A. Yamakage, "Analytic Theory of Edge Modes in Topological Insulators," J. Phys. Soc. Jpn. 79, 124709 (2010).
    3. S. Mao, A. Yamakage, and Y. Kuramoto, "Tight-binding model for topological insulators: Analysis of helical surface modes over the whole Brillouin zone," Phys. Rev. B 84, 115413 (2011).

  2. トポロジカル絶縁体薄膜における電子状態とトポロジカル相の制御

    トポロジカル絶縁体の表面状態は系の上面と下面の両方に存在する．したがって，薄膜にするとこれら２つの状態が混成する．この効果を用いて，薄膜系のギャップの大きさやトポロジカル相を制御することが可能になる．

    1. Kazuto Ebihara, Keiji Yada, Ai Yamakage, Yukio Tanaka, "Finite size effects of the surface states in a lattice model of topological insulator," Physica E 44, 885 (2012).

参考文献

  1. Y. Hatsugai, Phys. Rev. B 48, 11851 (1993); Y. Hatsugai, Phys. Rev. Lett. 71, 3697 (1993).
  2. Kentaro Nomura, Mikito Koshino, and Shinsei Ryu, Phys. Rev. Lett. 99, 146806 (2007).
戻る