トポロジカル絶縁体

ホール効果は磁場による電子のサイクロトロン運動により生じます． 量子ホール効果もやはり磁場が本質的に重要であり，実際，無磁場では量子ホール効果を示すようなトポロジカル相は存在しないのではないか，と考えられていました． しかしながら，2015年に Kane と Mele は，スピン軌道相互作用の強い二次元電子系（具体的にはグラフェン）が量子スピンホール効果を生じることを示し[1]，また，Z₂ (=0か1) のトポロジカル不変量によって保護されていることを明らかにしました[2]． 無磁場，すなわち時間反転対称性がある系でも起こる現象であり，さらに整数ではなく Z₂ 数で表されるというように，これは量子ホール効果とは全く異なる新しいトポロジカル相です．

最初に提案されたグラフェンは，実際には，スピン軌道相互作用が極めて小さいために量子スピンホール効果を実験的に観測するのは困難です． その後の研究により，スピン軌道相互作用が強い系である HgTe/CdTe 量子井戸[3]において，量子スピンホール効果を（間接的に）観測されました[4]． さらに，二次元だけではなく三次元の絶縁体も Z₂ のトポロジカル不変量を持っていることが理論的に示され[5]，実証されています[6]．

このような，Z₂ のトポロジカル不変量をもっている絶縁体はトポロジカル絶縁体と呼ばれています． ２次元のトポロジカル絶縁体では量子（スピン）ホール効果が生じました． 一方，３次元のトポロジカル絶縁体では，量子化された電気磁気交差応答，すなわち，

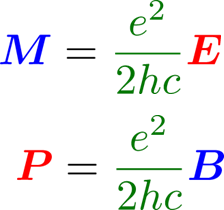
という特異な電磁応答が生じます[7]． ここで，M は磁化，P は電気分極，E は電場，B は磁場です． この係数（感受率） e²/2hc は物質の詳細に依らない普遍定数をとることがトポロジカル絶縁体の固有の興味深い性質（トポロジカル量子現象）です．

残念ながら，上記の量子化された電気磁気交差応答は現在のところ観測されてはいません．しかし，これ以外にもトポロジカルに非自明な電子状態に由来した現象が数多く議論されています． 我々もトポロジカル絶縁体における輸送現象について以下の研究を行っています．

1. "Charge transport in pn and npn junctions of silicene"
   A. Yamakage, M. Ezawa, Y. Tanaka, and N. Nagaosa,
   Phys. Rev. B 88, 085322 (2013).
   二次元のトポロジカル絶縁体物質であるシリセン（原子一層のシリコン）の pn 接合における電荷輸送．トポロジカルな電子状態に由来して，コンダクタンスが近似的に量子化される．
2. "Criticality of the metal–topological insulator transition driven by disorder", A. Yamakage, K. Nomura, K.-I. Imura, and Y. Kuramoto, Phys. Rev. B 87, 205141 (2013).
   "Disorder-Induced Multiple Transition involving Z2 Topological Insulator", A. Yamakage, K. Nomura, K.-I. Imura, and Y. Kuramoto, J. Phys. Soc. Jpn. 80, 053703 (2011).
   Most Cited Articles in 2012 from Vol. 80 (2011)
   現実の系には必ず存在する乱れの効果により，金属・絶縁体転移（アンダーソン局在）が起きる．この金属・絶縁体・トポロジカル絶縁体の相図の構造および金属絶縁体転移の臨界指数を決定した． また，通常の絶縁体に乱れを導入していくと， 通常絶縁体→金属→トポロジカル絶縁体という相転移が起こる． すなわち，乱れによってトポロジカル絶縁体を誘起することができる．
3. "Interfacial charge and spin transport in Z2 topological insulators", A. Yamakage, K.-I. Imura, J. Cayssol, and Y. Kuramoto, Phys. Rev. B 83, 125401 (2011).
   "Spin-orbit effects in a graphene bipolar pn junction", A. Yamakage, K.-I. Imura, J. Cayssol and Y. Kuramoto, Eur. Phys. Lett. 87, 47005 (2009).
   スピン軌道相互作用のあるグラフェンの pn 接合においては，波動関数の鏡映対称性に由来して，ラシュバスピン軌道相互作用（外部電場）によりコンダクタンスを 0 から 1 まで制御できる，という新しいタイプの輸送制御の方法を見出した．

参考文献

1. C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 226801 (2005).
2. C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005).
3. B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006).
4. M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X.-L. Qi, and S.-C. Zhang, Science 318, 766 (2007).
5. J. E. Moore and L. Balents, Phys. Rev. B 75, 121306(R) (2007); Rahul Roy, Phys. Rev. B 79, 195322 (2009); L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007).
6. D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature 452, 970 (2008).
7. X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Phys. Rev. B 78, 195424 (2008).